
The registration of non-rigidly deforming shapes is a fundamental problem in the area of Graphics and Computational Geometry. One of the applications of shape registration is to facilitate 3D model retrieval; after alignment it becomes easier to compare shapes since the correspondences between their elements is known. Many existing methods have been proposed for computing shape correspondence [van Kaick et al., 2011, Tam et al., 2013]. These approaches assume surface deformations to be either: piecewise rigid, (near-)isometric or topologically consistent. Presently, there are only a few public benchmarking shape correspondence datasets that challenge these assumptions about deformations [Bogo et al., 2014, Cosmo et al., 2016, Lähner et al., 2016, Andrews et al., 2018]. Previous contests [Cosmo et al., 2016, Lähner et al., 2016] have used synthetic objects that produce deformations that are not realistic. Bogo et al. [2014], Andrews et al. [2018] do capture real-life objects, they focus on specific object categories (human bodies and human faces), and neither benchmark suitably considers the different types of deformation that an object may undergo.
This motivates our competition which will provide of a new benchmark that consists of real-life shapes that undergo different types of deformations in a controlled manner. The competition will run at the Workshop on 3D Object Retrieval in Genova, Italy, 5-6 May 2019 and is collocated with Eurographics 2019.
To participate in this track, please register by emailing DykeRM@cardiff.ac.uk
For this track we have produced a new dataset from 3D scans of real-world objects, captured by ourselves using a high-precision 3D scanner (Artec3D Space Spider) designed for small objects. Each object exhibits one or more types of deformation. We classify these surface deformations into four distinct groups by level of complexity:
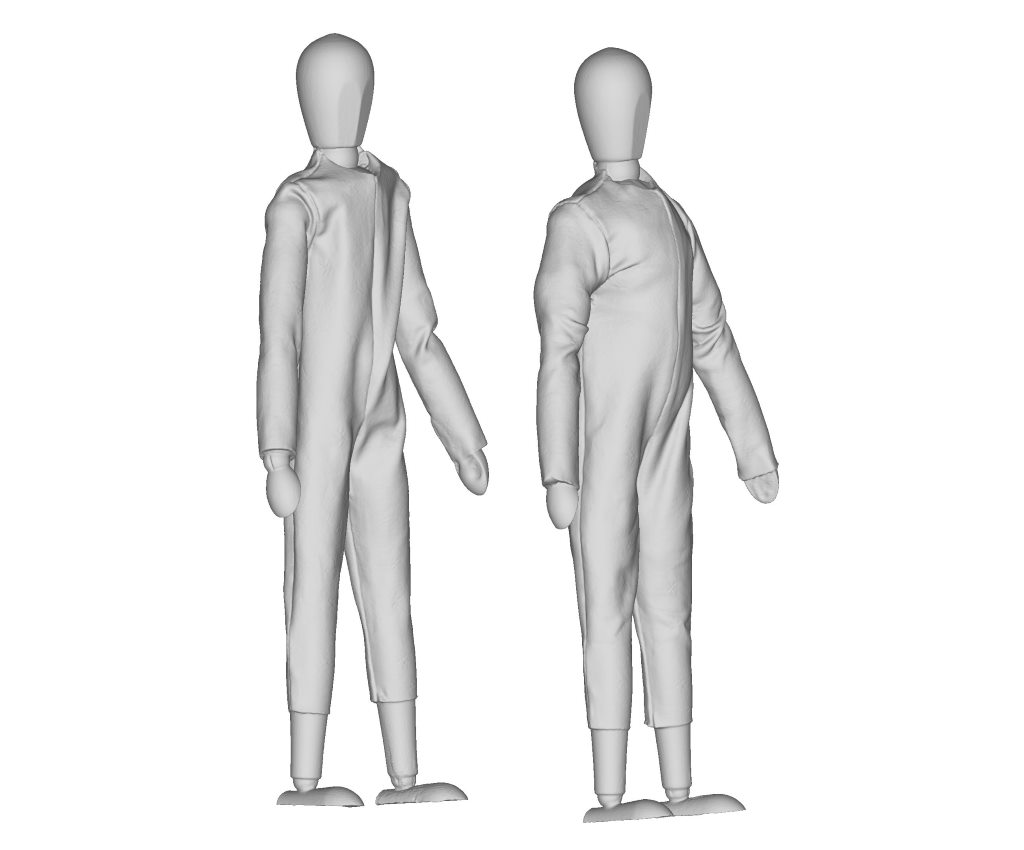
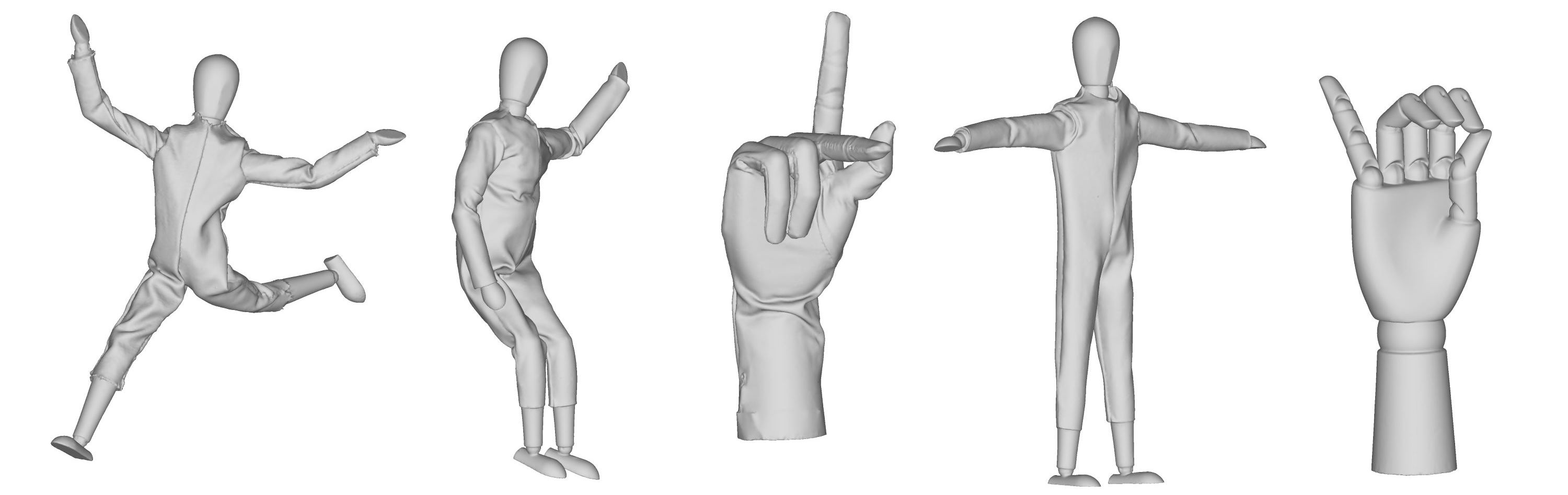
Non-isometric deformation
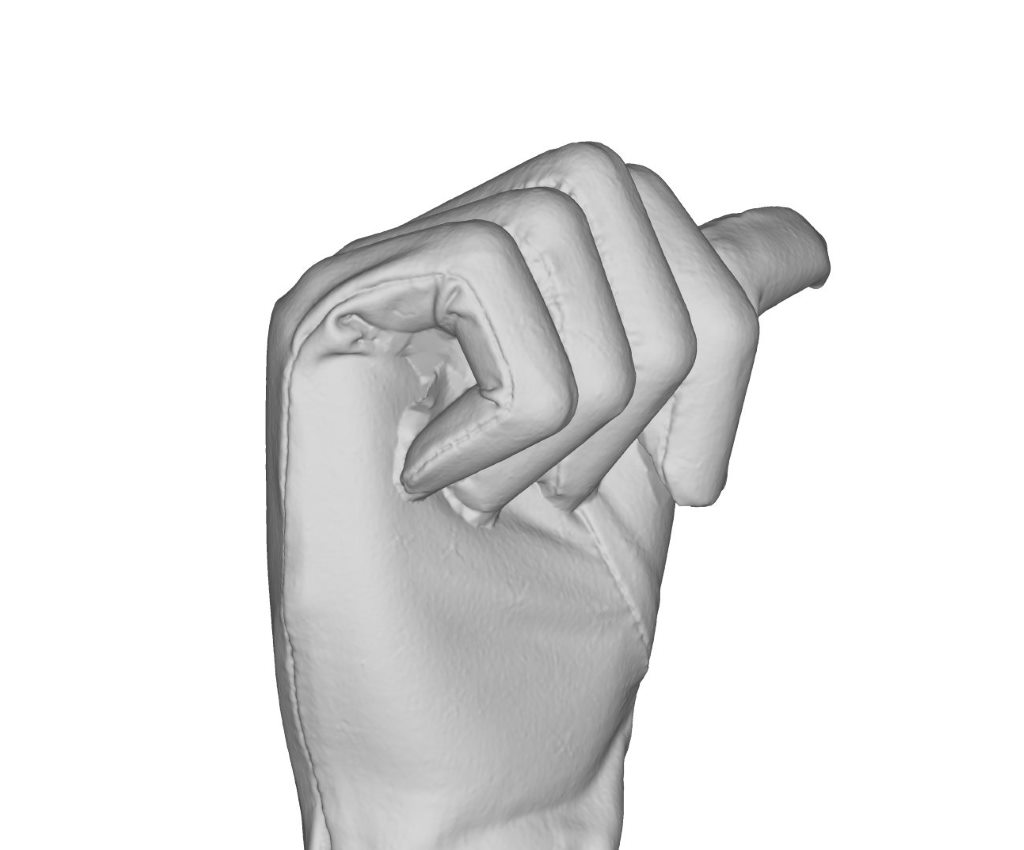
Geometric change caused by occlusion
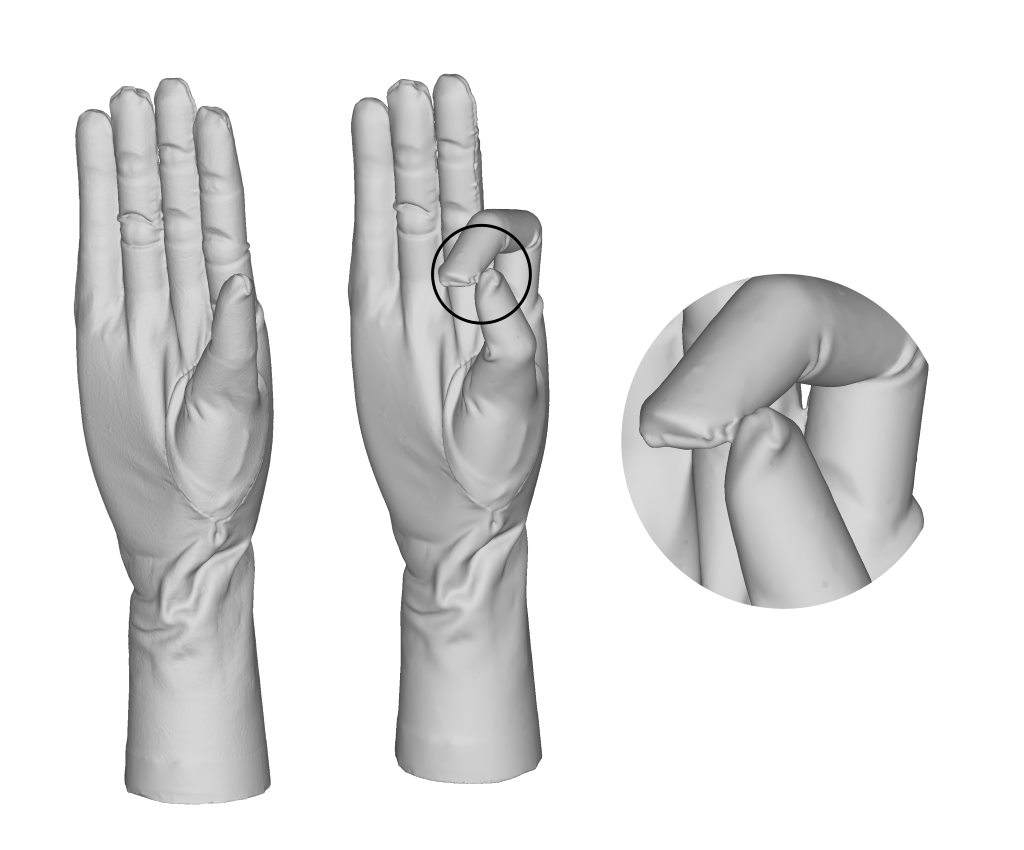
Topological change caused by self-contact
The dataset consists of wooden mannequins and wooden hands that are articulated. We have created clothes for the model from two materials; one that can bend but is resistant to stretching, and another that can bend and stretch. To induce greater non-isometry, we use plasticine underneath the clothing of the model. We have carefully selected objects and materials that incrementally introduce these deformation types so that the limitations (w.r.t. deformation type) can be clearly identified. Because the dataset consists of real-world scans, it contains geometric inconsistencies and topological change caused by self-contact of a shape. The real-scans also contain natural noise, varying triangulation of shapes and occluded geometry. Some examples of challenging cases are shown in the figure above.
The dataset contains 50 scans, and with 80 pairs of scans for the benchmark the dataset is a sufficient size for evaluative purposes. Pairs of scans have been split into four test-sets based on the types of deformation observed; participants will not be required to complete all test-sets and may submit one or more test-sets.
All scans are converted into triangulated and watertight meshes. Meshes are simplified to both 80,000 triangles and 20,000 triangles.
Ground-truth correspondences have been produced between surfaces of different scans of the same object using texture markers. These will not be made available to participants and are reserved for evaluation of contest entries.
Participants are provided a copy of the dataset and a list of mesh pairs for each test-set. Participants are to find the correspondence between shape pairs of one or more of the four test-sets. As well as their results, participants will be asked to also submit a description of the method used. Participants should mention any changes made to internal parameters between test-sets.
The quality of shape correspondence will be evaluated by the organisers automatically using normalised geodesics to measure the distance between the ground-truth and predicted correspondence. Similarly to other shape correspondence benchmarks [Cosmo et al., 2016, Lähner et al., 2016], we will evaluate the correspondence quality of each method using the approach of Kim et al. [2011]. We shall use the following measurements to help evaluate the performance of each method:
Let
be a pair of correspondences between target surface
and source surface
, the normalised geodesic error
between the predicted correspondence
and the ground-truth position
on surface
is measured as:
For methods that produce a sparse correspondence, we shall interpolate their result and measure the predicted correspondence against the ground truth.
Participants must complete one or more of the four test-sets. A short description of the algorithm/method used must be included with a submission. Either dense or sparse vertex-to-face correspondences for each mesh pair within a test-set may be submitted. Participants should email a zipped file containing their results to DykeRM@cardiff.ac.uk. If participants are unable send their results directly via email, e.g., because the file is too large, they may share their results via other platforms.
Each test set is a comma separated file, where each row represents a pair of shapes to be matched. Each file has two columns, the first indicates the source shape and the second indicates the target shape.
Like Cosmo et al. [2016], for each scan pair, participants shall give the correspondence for each vertex on the target shape to a barycentric co-ordinate on the source shape in a four column file, as follows:
The resulting correspondence between matched shape pairs must be stored in individual files. Preferably, all shape pair files will be listed in one root folder, results do not need to be split into individual tasks.
G. Andrews, S. Endean, R. Dyke, Y. Lai, G. Ffrancon, and G. K. L. Tam. HDFD - A high deformation facial dynamics benchmark for evaluation of non-rigid surface registration and classification. CoRR, abs/1807.03354, 2018. URL http://arxiv.org/abs/1807.03354.
F. Bogo, J. Romero, M. Loper, and M. J. Black. FAUST: Dataset and evaluation for 3D mesh registration. In Proceedings IEEE Conf. on Computer Vision and Pattern Recognition. IEEE, 2014. doi: 10.1109/CVPR.2014.491.
L. Cosmo, E. Rodolà, M. M. Bronstein, A. Torsello, D. Cremers, and Y. Sahillioğlu. Partial matching of deformable shapes. In Proceedings of the Eurographics 2016 Workshop on 3D Object Retrieval, 3DOR ’16, Goslar, Germany, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161089.
V. G. Kim, Y. Lipman, and T. Funkhouser. Blended intrinsic maps. In ACM SIGGRAPH 2011 Papers, SIGGRAPH ’11, pages 79:1–79:12, New York, NY, USA, 2011. ACM. ISBN 978-1-4503- 0943-1. doi: 10.1145/1964921.1964974.
Z. Lähner, E. Rodolà, M. M. Bronstein, D. Cremers, O. Burghard, L. Cosmo, A. Dieckmann, R. Klein, and Y. Sahillioglu. Matching of Deformable Shapes with Topological Noise. In Eurographics Workshop on 3D Object Retrieval, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161088.
G. K. L. Tam, Z. Cheng, Y. Lai, F. C. Langbein, Y. Liu, D. Marshall, R. R. Martin, X. Sun, and P. L. Rosin. Registration of 3d point clouds and meshes: A survey from rigid to nonrigid. IEEE Trans- actions on Visualization and Computer Graphics, 19(7):1199–1217, July 2013. ISSN 1077-2626. doi: 10.1109/TVCG.2012.310.
O. van Kaick, H. Zhang, G. Hamarneh, and D. Cohen-Or. A survey on shape correspondence. Computer Graphics Forum, 30(6):1681–1707, 2011. doi: 10.1111/j.1467-8659.2011.01884.x.
@inproceedings {Dyke:2019:track,
booktitle = {Eurographics Workshop on 3D Object Retrieval},
editor = {Biasotti, Silvia and Lavoué, Guillaume and Veltkamp, Remco},
title = {Shape Correspondence with Isometric and Non-Isometric Deformations},
author = {Dyke, R. M. and Stride, C. and Lai, Y.-K. and Rosin, P. L. and Aubry, M. and Boyarski, A. and Bronstein, A. M. and Bronstein, M. M. and Cremers, D. and Fisher, M. and Groueix, T. and Guo, D. and Kim, V. G. and Kimmel, R. and Lähner, Z. and Li, K. and Litany, O. and Remez, T. and Rodolà, E. and Russell, B. C. and Sahillioğlu, Y. and Slossberg, R. and Tam, G. K. L. and Vestner, M. and Wu, Z. and Yang, J.},
year = {2019},
publisher = {The Eurographics Association},
ISSN = {1997-0471},
ISBN = {978-3-03868-077-2},
DOI = {10.2312/3dor.20191069}
}